LORENZ ATTRACTOR

Ian Cooper

matlabvisualphysics@gmail.com

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

chaos23.m Lorenz attractor: Trajectories and animations

chaos23A.m Lorenz attractor: global bifurcation diagram

INTRODUCTION

In this article, I will show how Matlab can be used to visualize the solution of the Lorenz coupled ordinary differential equations for the Lorenz chaotic attractor. This system of equations was first described by Edward Lorenz in 1963. He was a M.I.T. meteorologist and mathematician who was interested in fluid flow models of the atmosphere.

A chaotic system is one that must show sensitivity to initial conditions, it must be

topologically mixing, its orbits must be dense, and for a short time the solutions will be nearly identical to one another and as time increases the trajectories of the chaotic systems will suddenly

have no correlation with the other and solutions will diverge no matter how small change is made to the initial conditions. The idea of topological mixing implies that the system will evolve over time such that every open set of its phase space will eventually intersect with every other open region. The density of the orbits is also of importance to prove that a system is acting chaotically. Orbits may never come close to anything resembling repeating themselves.

The equations describing the Lorenz chaotic attractor are:

Parameters

is the Prandtl number and it represents the ratio of fluid viscosity to thermal conductivity, essentially the ratio of how quickly fluid flows through the system to how effective it absorbs heat in contact with other molecules

is the normalized Rayleigh number (main variable that is usually varied) and it represents the difference in temperature between the top and bottom of the atmospheric column

depends upon the geometry of the domain and simply describes the bounds of the system.

The most popular values for the parameters are:

x, y, z

The x and y parameters relate to the vertical and horizontal temperature variations in the atmosphere respectively, and the z component is related to the convection in atmospheric flow.

x, y, z all vary dynamically in time.

x is the convective flow (motion of heat through the atmosphere as hot air rises), positive x pertains to clockwise motion.

y is the horizontal temperature distribution, found by taking the difference between ascending and descending currents, positive y pertains to warmer currents on the right (correlates strongly with positive x)

z is the vertical temperature distribution.

For some values of the three parameters , the trajectory is bounded, but not periodic, and not convergent as it ranges chaotically back and forth between two attractors (critical points) – strange attractors. For other values, the solution might diverge to infinity, converge to a fixed point or oscillate periodically.

Critical points (fixed points)

There are three fixed points, x_C, y_C, and z_C where the x, y and z parameters are constant

An obvious critical point is the Origin (0, 0, 0). To find the other critical points, we can take the y_C component as a free parameter such that

then the other fixed points or critical points are

x_C = y_C and

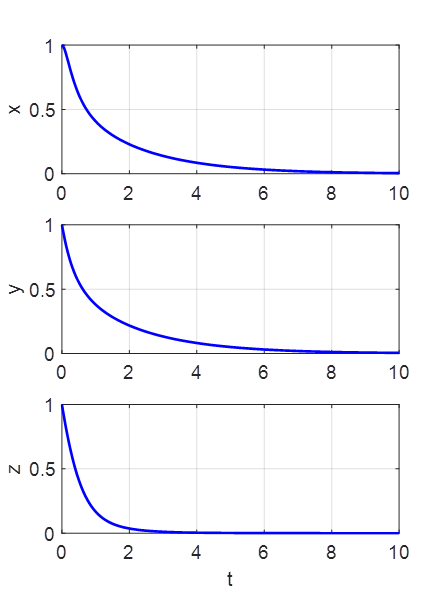
All three fixed points are unstable. If the initial position corresponds to a fixed point, the values of x, y, and z never change. However, even a small deviation in starting values from a fixed point will cause the system to evolve so that the trajectory will always be repelled from a fixed point if it tries to approach it.

If then the Origin is a global attractor and the motion freezes at the Origin.

The system of the three coupled ordinary differential equations is solved using the Matlab command ode45. The Script chaos23.m facilitates simulations with the Lorenz equations. Model parameters are changed in the INPUT section of the Script and the results are displayed in a series of Figure Windows.

Significance of Lorenz in Atmospheric Dynamics

· Allows us to see how different emissions spread by convection through the atmosphere.

· Allows us to model weather and wind more accurately.

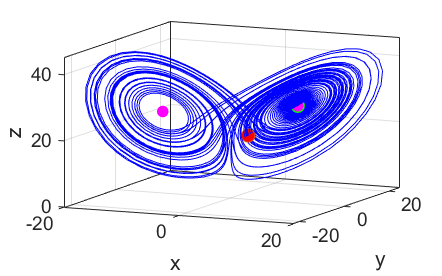
· Allows us to model the effect of anthropogenic emissions on vertical and horizontal temperature gradients.

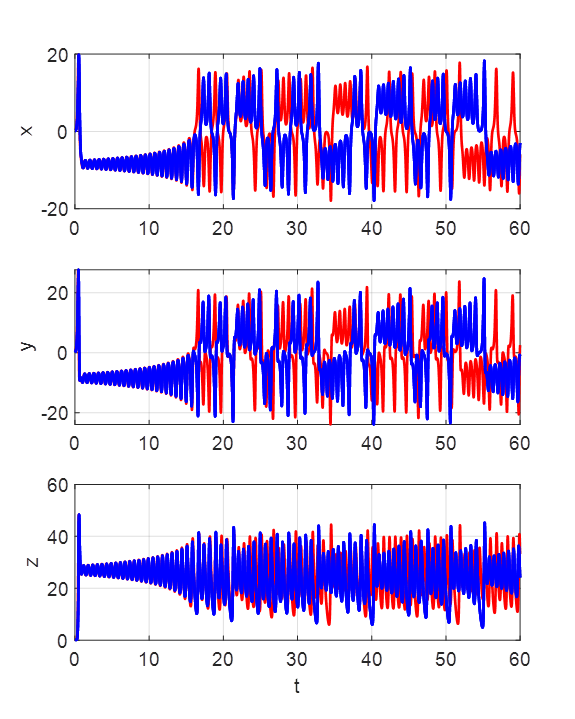
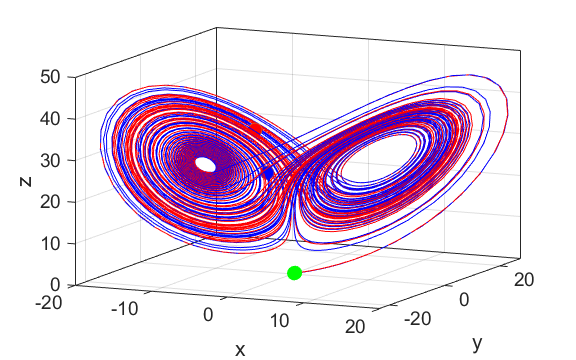
SIMULATION 1

The Script is run with two slightly different sets of initial conditions. Initially the oscillations are very similar but after about 15 time-units, the motions diverge and both become chaotic.

Parameters:

Initial displacements blue

red

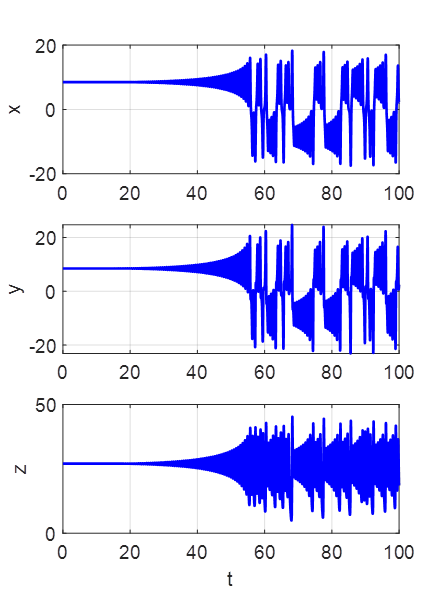
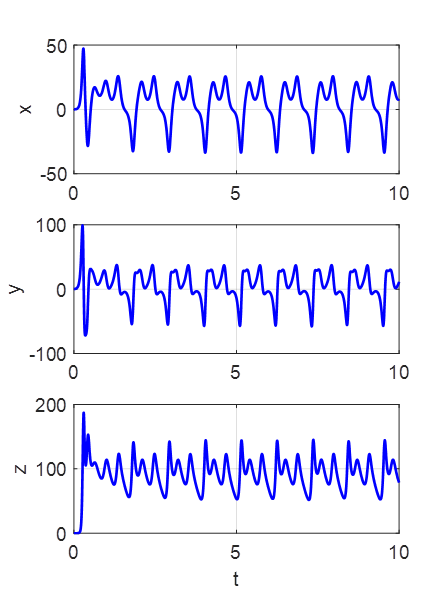
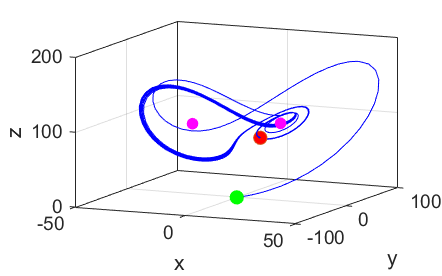
SIMULATION 2

The initial displacement is set at the fixed point

x0 = 8.485281374238570

y0 = 8.485281374238570

z0 = 27

for the parameters .

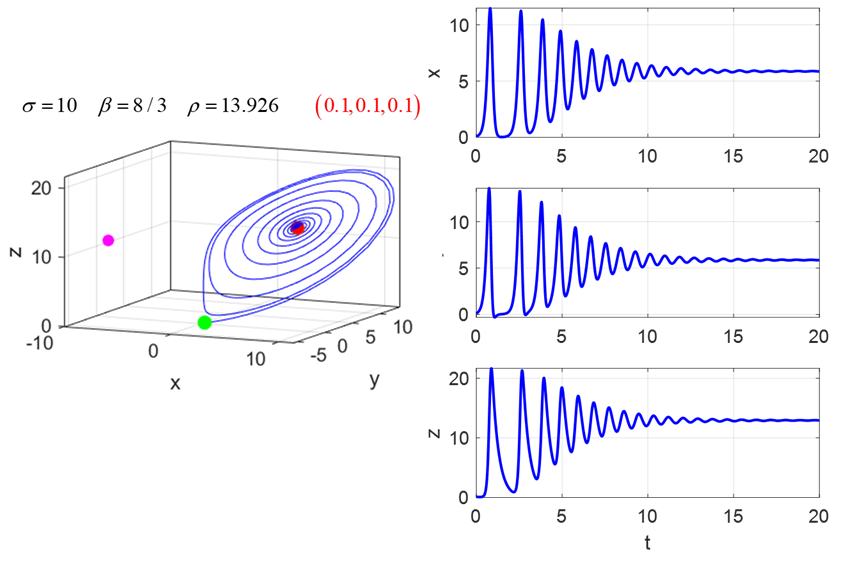
For a long period, the trajectory oscillates around the starting fixed point. However, as the trajectory approaches this fixed point it is always repelled, leading to chaotic motion as it later oscillates around the both of the fixed points for ever. The trajectory is completely determined by the initial starting position. The motion is not random but it is not predictable.

SIMULATION 3

For the parameters the motion becomes periodic after the initial transience – the motion is not chaotic.

SIMULATION 4

If the Rayleigh number then the Origin is a global attractor and the motion freezes at the Origin.

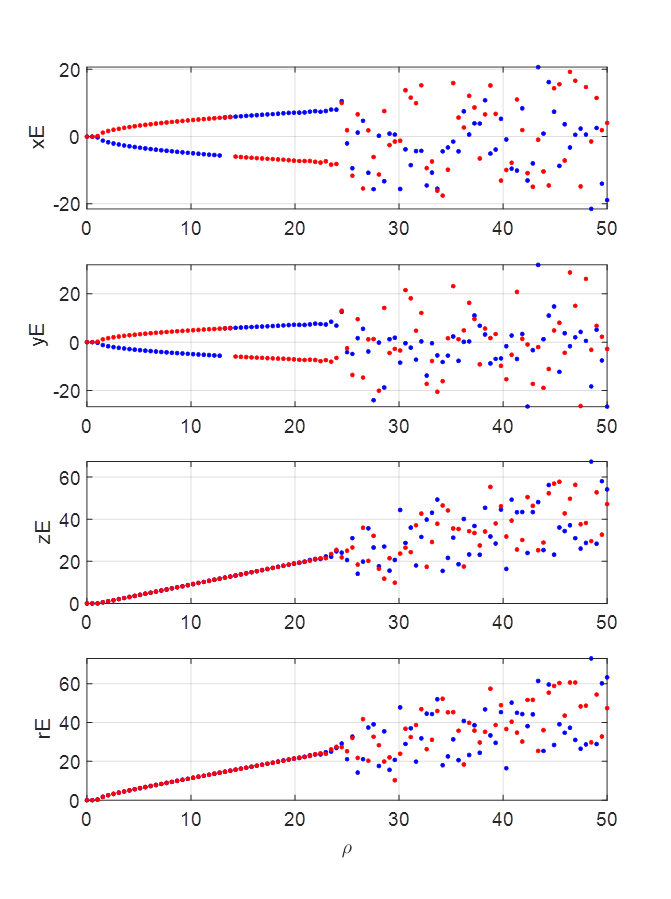
SIMULATION 5 Global bifurcations

Initial conditions

The values xE, yE, zE and are the final displacement values at the end of the simulation when tE = 20.

Another interesting behaviour is that there exists a homoclinic bifurcation.

If you start near the Origin and follow the unstable manifold trajectory outward, you’ll eventually end up attracting to a limit cycle in one of the two “lobes” when is small. As increases, the limit cycle grows until it intersects with the saddle point at the Origin for ≈ 13.926. This is called a homoclinic orbit. For , the dynamics is chaotic.

REFERENCES

https://www.youtube.com/watch?v=Q_f1vRLAENA

https://ocw.mit.edu/courses/res-18-009-learn-differential-equations-up-close-with-gilbert-strang-and-cleve-moler-fall-2015/